Deep learning笔记4-TreeRNN递归神经网络
1. 递归神经网络(TreeRNN)
原图和公式以及说明来自:零基础入门深度学习(5) - 循环神经网络
RNN循环神经网络处理词序列,但有时候把句子看做是词的序列是不够的,比如『两个外语学院的/学生』与『两个/外语学院的学生』意思不同,为了能够让模型区分出两个不同的意思,模型可借助树结构去处理信息,而不是序列,这就是递归神经网络的作用。当面对按照树/图结构处理信息更有效的任务时,递归神经网络通常都会获得不错的结果。
TreeRNN递归神经网络可以把一个树/图结构信息编码为一个向量,也就是把信息映射到一个语义向量空间中。这个语义向量空间满足某类性质,比如语义相似的向量距离更近。如果两句话(尽管内容不同)它的意思是相似的,那么把它们分别编码后的两个向量的距离也相近;反之就远。如下图所示:
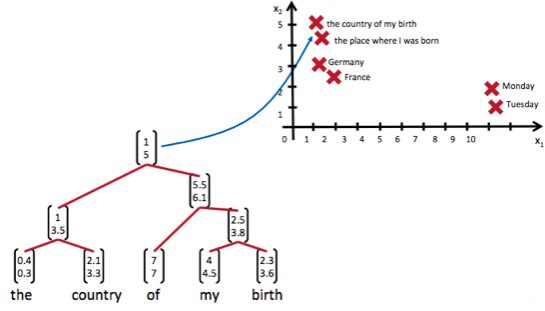
递归神经网络可以将词、句、段、篇按照他们的语义映射到同一个向量空间中,也就是把可组合(树/图结构)的信息表示为一个个有意义的向量。
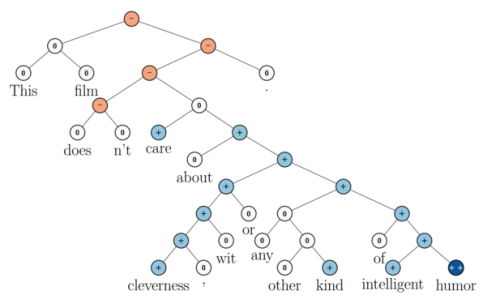
蓝色表示正面评价,红色表示负面评价。每个节点是一个向量,这个向量表达了以它为根的子树的情感评价。比如"intelligent humor"是正面评价,而"care about cleverness wit or any other kind of intelligent humor"是中性评价。可以看到,模型能够正确的处理doesn't的含义,将正面评价转变为负面评价。
尽管递归神经网络具有更为强大的表示能力,但是在实际应用中并不太流行。其中一个主要原因是,递归神经网络的输入是树/图结构,而这种结构需要花费很多人工去标注。
1.1. 递归神经网络输出值的计算(正向)
递归神经网络的输入是两个子节点(也可以是多个),输出就是将这两个子节点编码后产生的父节点,父节点的维度和每个子节点是相同的。如下图所示:
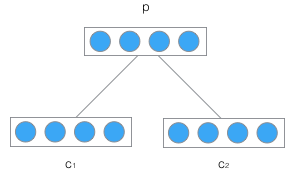
C1和C2分别是表示两个子节点的向量,P是表示父节点的向量。子节点和父节点组成一个全连接神经网络,也就是子节点的每个神经元都和父节点的每个神经元两两相连。用矩阵W表示这些连接上的权重,它的维度将是d*2d,其中,d表示每个节点的维度。父节点的计算公式可以写成:
\[\begin{align} \mathbf{p} = tanh(W\begin{bmatrix}\mathbf{c}_1\\\mathbf{c}_2\end{bmatrix}+\mathbf{b}) \end{align}\]
在上式中,tanh是激活函数(当然也可以用其它的激活函数),b是偏置项,它也是一个维度为d的向量。
然后,把产生的父节点的向量和其他子节点的向量再次作为网络的输入,再次产生它们的父节点。如此递归下去,直至整棵树处理完毕。最终,将得到根节点的向量,可以认为它是对整棵树的表示,这样就实现了把树映射为一个向量。在下图中使用递归神经网络处理一棵树,最终得到的向量(整棵树)的表示:
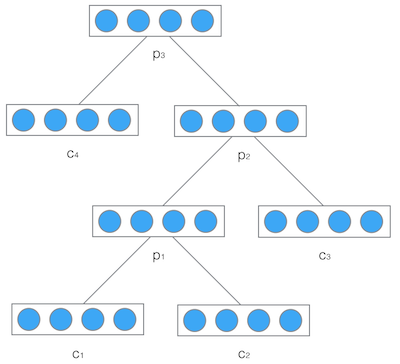
递归神经网络的权重w和偏置项b在所有的节点都是共享的。
1.2. 递归神经网络的训练(反向)
递归神经网络的训练算法BPTS和循环神经网络类似,两者不同之处在于:
● 前者需要将残差从根节点反向传播到各个子节点
● 后者是将残差从当前时刻反向传播到初始时刻
误差项从父节点传递到其子节点的公式:
\[\begin{align} \delta_{c_j}&=\frac{\partial{E}}{\partial{\mathbf{net}_{c_j}}}\\ &=\frac{\partial{E}}{\partial{\mathbf{c}_j}}\frac{\partial{\mathbf{c}_j}}{\partial{\mathbf{net}_{c_j}}}\\ &=W_j^T\delta_p\circ f'(\mathbf{net}_{c_j}) \end{align}\]
● 误差函数在第l层对权重的梯度为:
\[\begin{align} \frac{\partial{E}}{\partial{w_{ji}^{(l)}}}&=\frac{\partial{E}}{\partial{\mathbf{net}_{p_j}^{(l)}}}\frac{\partial{\mathbf{net}_{p_j}^{(l)}}}{\partial{w_{ji}^{(l)}}}\\ &=\delta_{p_j}^{(l)}c_i^{(l)}\\ \end{align}\]
权重梯度是各个层权重梯度之和。即:
\[\begin{align} \frac{\partial{E}}{\partial{W}}=\sum_l\frac{\partial{E}}{\partial{W^{(l)}}} \end{align}\]
如果使用梯度下降优化算法,那么权重更新公式为: \[\begin{align} W\gets W + \eta\frac{\partial{E}}{\partial{W}} \end{align}\]
● 误差函数对第l层偏置项的梯度为:
\[\begin{align} \frac{\partial{E}}{\partial{b_j^{(l)}}}&=\frac{\partial{E}}{\partial{\mathbf{net}_{p_j}^{(l)}}}\frac{\partial{\mathbf{net}_{p_j}^{(l)}}}{\partial{b_j^{(l)}}}\\ &=\delta_{p_j}^{(l)}\\ \end{align}\]
偏置项梯度是各个层偏置项梯度之和,即:
\[\begin{align} \frac{\partial{E}}{\partial{\mathbf{b}}}=\sum_l\frac{\partial{E}}{\partial{\mathbf{b}^{(l)}}} \end{align}\]
如果使用梯度下降优化算法,那么偏置项更新公式为: \[\begin{align} \mathbf{b}\gets \mathbf{b} + \eta\frac{\partial{E}}{\partial{\mathbf{b}}} \end{align}\]
2. 相关应用
2.1 在自然语言处理的应用(NLP)
递归神经网络能够完成句子的语法分析,产生一颗语法解析树。
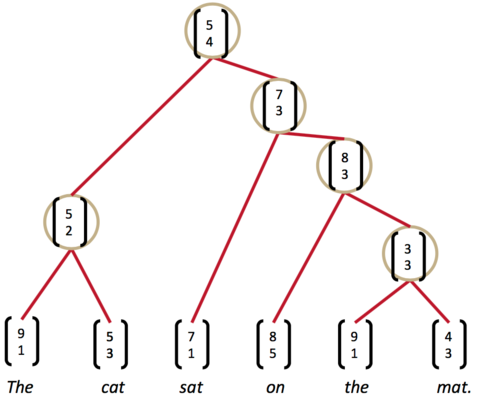
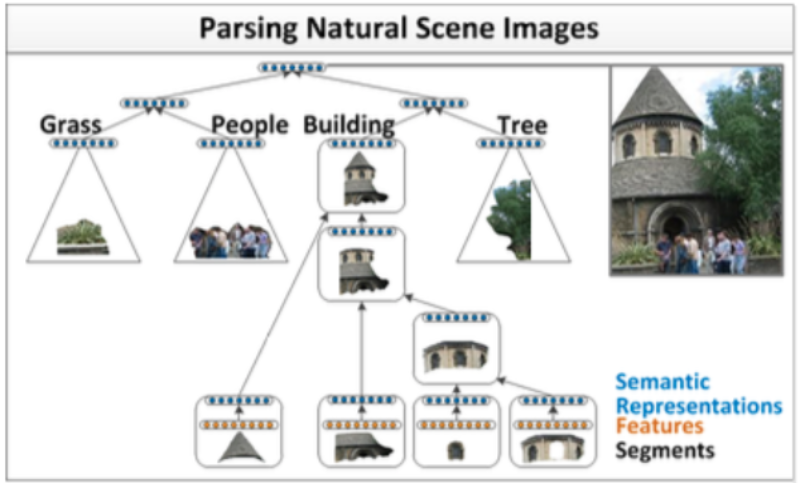
2.1 在自然场景的应用
除了自然语言之外,自然场景也具有可组合的性质。因此可以用类似的模型完成自然场景的解析,如下图所示: